Задание 1.

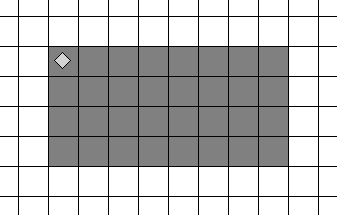
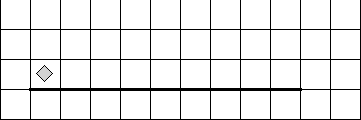
На поле Робота стен нет. Робот находится в левом верхнем углу прямоугольника из закрашенных клеток. Размеры прямоугольника неизвестны. Составь алгоритм, переводящий Робота в правыйнижний угол прямоугольника.

 

 

Задание 2. Составь алгортмы со следующими заголовками:

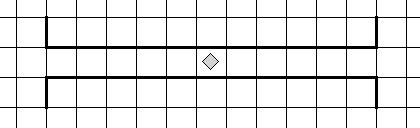
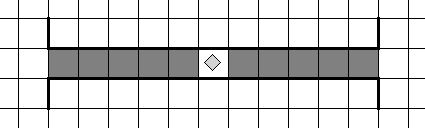
а) алг закрасить коридор
. дано| Робот где-то в горизонтальном коридоре
. надо| закрашены все клетки коридора, кроме стартовой (клетки А), Робот в исходном положении

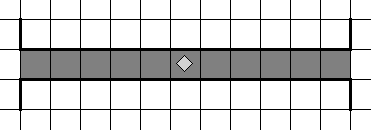
б) алг закрасить коридор
. дано| Робот где-то в горизонтальном коридоре
. надо| закрашены все клетки коридора, Робот в исходном положении

 

в) алг закрасить ряд
. дано| Робот на­хо­дит­ся свер­ху от горизонтальной стены в левом её конце, длина стены неизвестна
. надо| закрашены все клетки, рас­по­ло­жен­ные выше стены на рас­сто­я­нии одной пу­стой клет­ки от стены

 

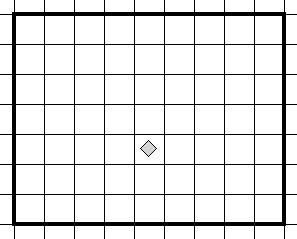
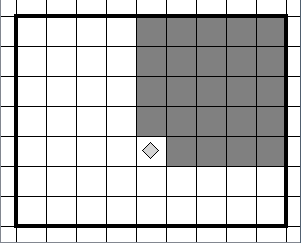
г) алг закрасить угол
. дано| Робот внутри прямоугольника, огороженного стенами
. надо| закрашены все клетки правее и выше стартовой, Робот в исходном положении

 

 

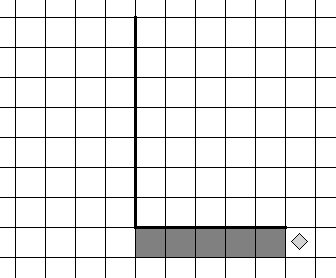
Задание 3*.  На бес­ко­неч­ном поле име­ет­ся вер­ти­каль­ная стена. Длина стены неизвестна. От ниж­не­го конца стены впра­во от­хо­дит го­ри­зон­таль­ная стена также не­из­вест­ной длины. Робот на­хо­дит­ся в клетке, рас­по­ло­жен­ной слева от вер­ти­каль­ной стены и выше го­ри­зон­таль­ной стены. На ри­сун­ке ука­зан один из воз­мож­ных спо­со­бов рас­по­ло­же­ния стен и Ро­бо­та (Робот обо­зна­чен ромбиком).

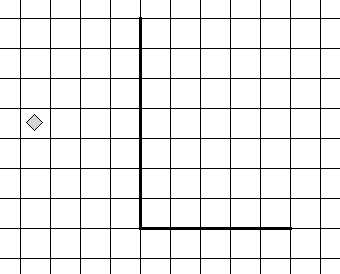
Напиши для Ро­бо­та алгоритм, за­кра­ши­ва­ю­щий все клетки, рас­по­ло­жен­ные ниже го­ри­зон­таль­ной стены и при­мы­ка­ю­щие к ней. Тре­бу­ет­ся за­кра­сить толь­ко клетки, удо­вле­тво­ря­ю­щие дан­но­му условию. Например, для приведённого выше ри­сун­ка Робот дол­жен за­кра­сить сле­ду­ю­щие клет­ки (см. рисунок).

 

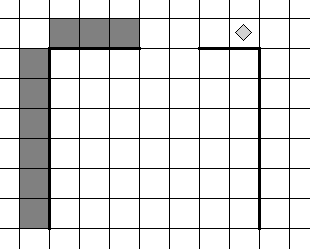
Задание 4*. На поле име­ет­ся стена, длины от­рез­ков стены неизвестны. Стена со­сто­ит из двух вер­ти­каль­ных и со­еди­ня­ю­ще­го их го­ри­зон­таль­но­го от­рез­ков (отрезки стены рас­по­ло­же­ны «буквой П»). В го­ри­зон­таль­ном участ­ке есть ровно один проход, место и длина про­хо­да неизвестны. Робот на­хо­дит­ся в клетке, рас­по­ло­жен­ной над пра­вым кон­цом го­ри­зон­таль­но­го от­рез­ка стены.

На ри­сун­ке ука­зан один из воз­мож­ных спо­со­бов рас­по­ло­же­ния стен и Робота (Робот обо­зна­чен ромбиком).

Напиши для Ро­бо­та алгоритммбиком, за­кра­ши­ва­ю­щий все клетки, рас­по­ло­жен­ные над го­ри­зон­таль­ным от­рез­ком стены слева от прохода, и все клетки, рас­по­ло­жен­ные с внеш­ней сто­ро­ны от ле­во­го вер­ти­каль­но­го участ­ка стены. Робот дол­жен за­кра­сить толь­ко клетки, удо­вле­тво­ря­ю­щие дан­но­му условию.

Например, для приведённого спра­ва ри­сун­ка Робот дол­жен за­кра­сить сле­ду­ю­щие клет­ки (см. рисунок).

 

 

Задание 5*. На бес­ко­неч­ном поле име­ет­ся стена, со­сто­я­щая из 5 по­сле­до­ва­тель­ных отрезков, рас­по­ло­жен­ных змейкой: вправо, вниз, влево, вниз, вправо, все от­рез­ки неизвестной длины. Робот на­хо­дит­ся в самой левой клет­ке непосредственно под верх­ней горизонтальной стеной. На ри­сун­ке указан один из воз­мож­ных способов рас­по­ло­же­ния стен и Ро­бо­та (Робот обо­зна­чен ромбиком).

Напиши для Ро­бо­та алгоритм, за­кра­ши­ва­ю­щий все клетки, рас­по­ло­жен­ные ниже пер­во­го и левее вто­ро­го отрезков стены и левее четвёртого и ниже пя­то­го отрезков стены. Робот дол­жен закрасить толь­ко клетки, удо­вле­тво­ря­ю­щие данному условию. Например, для приведённого выше ри­сун­ка Робот дол­жен закрасить сле­ду­ю­щие клетки (см. рисунок).